چگونه مشتق را مفهومی یاد بگیریم؟

یادگیری مشتق یکی از مهمترین بخشهای ریاضی دبیرستان و کنکور است؛ چون هم درک عمیقتری از رفتار توابع میدهد و هم پایهی بسیاری از مباحث پیشرفتهتر مانند بهینهسازی، نرخ تغییرات و بررسی نمودارهاست. بسیاری از داوطلبان در ابتدا تصور میکنند مشتق مبحثی پیچیده است، اما اگر مفهومی یاد گرفته شود، به یکی از شیرینترین و کاربردیترین بخشهای ریاضی تبدیل خواهد شد. در این مسیر، داشتن یک منبع درست و یک مدرس که مفاهیم را شفاف و مرحلهبهمرحله توضیح دهد، اهمیت زیادی دارد. از همینرو، استاد امید سلمانی با آموزشهای دقیق و قابلفهم خود، یادگیری مشتق را برای دانشآموزان سادهتر و قابل دسترستر کرده است.
روش یادگیری مشتق گیری در یک نگاه
| مرحله | تمرین و روش مطالعه |
|---|---|
| 1. یادگیری مفاهیم پایهای و پیشنیازها | مثالهای ساده و تمرینهای کاربردی برای تثبیت مفاهیم |
| 2. یادگیری قواعد مشتقگیری | حل تست آموزشی بلافاصله بعد از یادگیری هر قاعده |
| 3. یادگیری مشتق دوازدهم | حل تستهای ترکیبی و مرور مداوم با روش مطالعه ریاضی کنکور |
| 4. تمرین کاربردی و حل تست | تحلیل آزمون: بررسی اشتباهات و رفع نقاط ضعف |
| 5. مرور و تثبیت | مرور منظم مباحث، حل تستهای اشتباه و بازآموزی |
روش یادگیری مشتق بهصورت مفهومی
بسیاری از دانشآموزان در ابتدا مشتق را به عنوان یک مجموعه فرمول و قواعد خشک میبینند، اما واقعیت این است که اگر مفهومی و مرحلهبهمرحله آموزش داده شود، تبدیل به یکی از شیرینترین و کاربردیترین بخشهای ریاضی میشود. درک صحیح از مشتق نه تنها برای حل تستهای کنکور بلکه برای مباحث پیشرفتهتر مانند بهینهسازی و نمودار توابع بسیار ضروری است. در این مسیر، منابع آموزشی مناسب و پکیج هیولا استاد امید سلمانی میتوانند نقش بسیار مهمی در تثبیت یادگیری داشته باشند و با تحلیل آزمون، نقاط ضعف و قوت شما را به خوبی مشخص کنند. در ادامه، مراحل یادگیری مشتق از پایه به شیوه مفهومی و کاربردی توضیح داده میشوند.

مرحله 1؛ یادگیری مفاهیم پایهای و پیشنیازها
برای شروع یادگیری مشتق، ابتدا باید مفاهیم پایه را به خوبی درک کنید. این مرحله شامل موارد زیر است:
- تابع و نمودار تابع: قبل از مشتق، باید بدانید تابع چیست و چگونه رفتار آن را در نمودار مشاهده میکنید.
- حد و پیوستگی: مفهوم تغییرات بسیار کوچک و نقطهای که تابع در آن تعریف شده است، پایهای برای درک مشتق است.
- تغییرات و نرخ رشد: درک این که مشتق نشاندهنده نرخ تغییر یک تابع است، کلید یادگیری مفهومی مشتق است.
با تمرینهای ساده و مثالهای کاربردی، یادگیری مشتق از پایه محقق میشود و شما آماده ورود به قواعد مشتقگیری خواهید شد.
مرحله 2؛ یادگیری قواعد مشتقگیری
پس از درک مفاهیم پایه، باید با یادگیری مشتق گیری شروع کنید:
- قواعد ساده: مشتق جمع، تفریق و ضرب ثابتها.
- مشتق توابع پایه: توابع چندجملهای، توابع نمایی و توابع لگاریتمی.
- مشتق توابع ترکیبی و تابع مرکب: استفاده از قانون زنجیرهای و مشتق توابع چندمرحلهای.
در این مرحله، تمرین و حل تستهای آموزشی اهمیت بسیار بالایی دارد. ب
مرحله 3؛ یادگیری مشتق دوازدهم
در این مرحله، به مباحث پیشرفتهتر مانند مشتق توابع مثلثاتی و کاربردهای آنها میپردازید.
- مشتق توابع مثلثاتی: سینوس، کسینوس و تانژانت.
- کاربرد مشتق: بررسی نقاط بحرانی، بیشینه و کمینه تابع، و بررسی نمودار.
- تمرین ترکیبی: تستهایی که چند قاعده را در یک سؤال ترکیب میکنند.
تمرین منظم و استفاده از بهترین روش مطالعه ریاضی کنکور باعث میشود این مباحث برای شما ملموس و قابل حل شوند.
مرحله 4؛ تمرین کاربردی و حل تست
هیچ یادگیری مفهومی بدون تمرین کافی کامل نمیشود.
- حل تستهای طبقهبندی شده و تمرین ترکیبی برای تثبیت مفاهیم.
- پس از هر تست یا آزمون، اشتباهات خود را بررسی و علت آنها را مشخص کنید.
- مرور تستهای اشتباه و تمرین دوباره برای تثبیت کامل مطالب.
مرحله 5؛ مرور و تثبیت
یادگیری مشتق نیاز به مرور مداوم دارد:
- مرور هفتگی و ماهانه مباحث یاد گرفته شده.
- حل تستهای زماندار برای افزایش سرعت و دقت.
- تمرکز روی آسان ترین مباحث ریاضی برای مطالعه در کنکور در طول مرورها برای تقویت روحیه و پیشرفت سریع.
با این روش، یادگیری مشتق نه تنها مفهومی و اصولی خواهد بود، بلکه درصدگیری شما در کنکور نیز بهبود چشمگیری خواهد یافت.
برای موفقیت در یادگیری مشتق، باید از پایه شروع کنید، مفاهیم اصلی را بفهمید، قواعد مشتقگیری را تمرین کنید، تستهای آموزشی و زماندار حل کنید و ارتباط مشتق با انتگرال را درک کنید. استفاده از تحلیل دقیق آزمونها مسیر یادگیری شما را هموار و تضمینشده میکند. این روش جامع باعث میشود که حتی سختترین تستها هم قابل حل شوند و درصد شما در درس ریاضی بهبود چشمگیری پیدا کند.
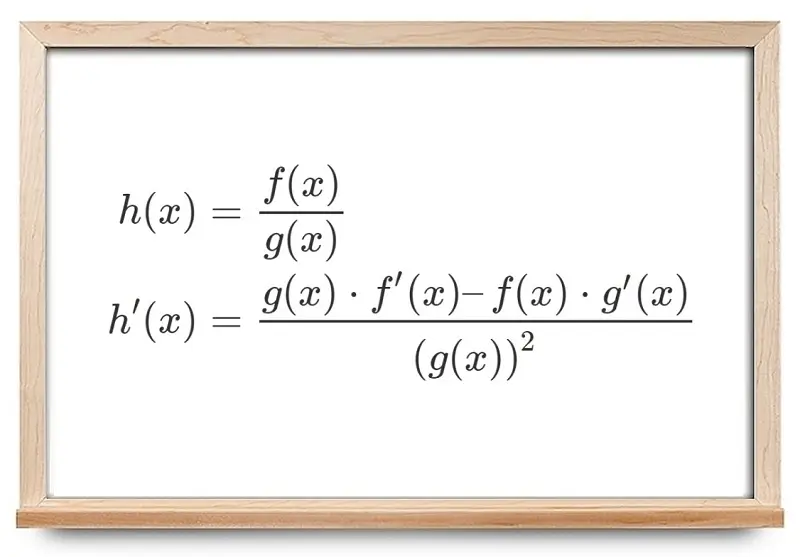
کاربرد مشتق در ریاضی و حل مسائل کنکور
کاربرد مشتق در ریاضی و حل مسائل کنکور بسیار گسترده است و یکی از مباحث کلیدی در درس ریاضی به شمار میرود. مشتق به شما کمک میکند تا رفتار توابع را تحلیل کنید و تغییرات آنها را به صورت دقیق درک کنید. یکی از مهمترین کاربردهای مشتق، یافتن نقاط بحرانی توابع است که برای تعیین بیشینه و کمینه تابع استفاده میشود. این مهارت در مسائل بهینهسازی، اقتصاد و فیزیک کاربرد مستقیم دارد.
علاوه بر آن، مشتق برای بررسی نمودار توابع و شناخت رفتار صعودی یا نزولی یک تابع اهمیت دارد. با محاسبه مشتق، میتوان فهمید که تابع در کدام بازهها افزایش یا کاهش دارد و این اطلاعات در حل تستهای کنکور به شدت کارآمد است. در رشتههای علوم تجربی و ریاضی، مشتق برای محاسبه سرعت و شتاب، نرخ تغییرات و تحلیل پدیدههای طبیعی کاربرد دارد. همچنین، یادگیری مشتق، مسیر ورود به مباحث انتگرال و ریاضیات پیشرفته را هموار میکند و درک مفهومی از تغییرات پیوسته را ممکن میسازد.
برای داوطلبان کنکور، تمرین تستهای مختلف مشتق و تحلیل آزمون کمک میکند تا بتوانند در کوتاهترین زمان، بیشترین درصد را کسب کنند. در نهایت، تسلط بر مشتق نه تنها درصد شما را در درس ریاضی افزایش میدهد، بلکه توانایی تحلیل مسائل واقعی و پیشرفت در مباحث پیشرفته ریاضی را نیز فراهم میکند.
سوالات متداول
چرا یادگیری مشتق به صورت مفهومی مهم است؟
یادگیری مفهومی مشتق باعث میشود بتوانید تغییرات توابع را بهدرستی تحلیل کنید و تستهای دشوار را بدون حفظ فرمولهای بیفایده حل کنید. این روش، پایهای برای فهم انتگرال و مباحث پیشرفتهتر ریاضی است.
از کجا باید یادگیری مشتق را شروع کنم؟
ابتدا مفاهیم پایهای مانند تابع، نمودار تابع، حد و پیوستگی و نرخ تغییر را یاد بگیرید. درک این مفاهیم، یادگیری قواعد مشتقگیری را بسیار سادهتر میکند.
بهترین روش یادگیری قواعد مشتق چیست؟
قواعد ساده (جمع، تفریق، ضرب ثابتها)، مشتق توابع پایه (چند جملهای، نمایی، لگاریتمی) و مشتق توابع مرکب با استفاده از قانون زنجیرهای را مرحلهبهمرحله تمرین کنید و بعد از هر مبحث تست آموزشی حل کنید.






دیدگاهتان را بنویسید